In-memory computing (IMC) aims to speed up computation on data by reducing the physical distance between data and computation as much as possible. The motivation for this approach came from the realization that in von-Neumann architectures processing large amounts of data often has a speed and energy bottleneck in memory accesses. This is also known as the von Neumann bottleneck or memory wall. In its purest definition IMC only includes architectures where the computation takes place within the memory devices. While both charge-based and resistance-based memory devices are considered for IMC, especially research on nonvolatile memristive memories got a lot of attention in recent years.
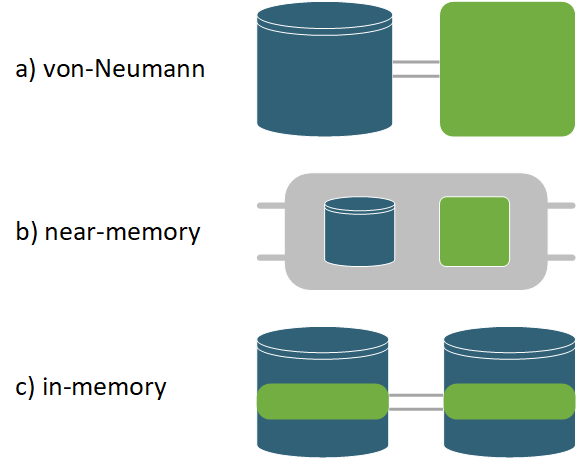
In a broader interpretation of IMC the term is often stretched to near-memory computing or processing in memory (PIM) architectures for which it can already be sufficient that the memory and processors are on the same chip. Stricter definitions require a certain degree of memory distribution with specialized local memories per processor to reduce memory access latency and energy consumption.
Crossbar computation
The most prominent form of IMC is crossbar computation, because of its suitability to parallelize multiply-accumulate (MAC) operations, which are for example needed for vector-matrix and matrix-matrix multiplications. In a crossbar the memory devices are arranged in rows and columns. While rows are provided with input data, each device in a row performs its atomic computational operation with the input data and data stored in the device itself. Typically this is a multiply operation. When emerging resistive non-volatile memories are used, the input is provided as a voltage and the output current of the device is the result of the analog multiplication of the input voltage and the devices resistance according to Ohm’s law. The programmable device resistance is the data stored on the device.
The output is then provided to the device’s column of the crossbar where the column performs its atomic computational operation to create one result per column. Typically this is an accumulate operation, which sums up all results from the column’s devices. In case of the previous example with resistive memory devices and input voltages the device results are currents, which are directly summed up according to Kirchhoff’s law by connecting the device outputs together.
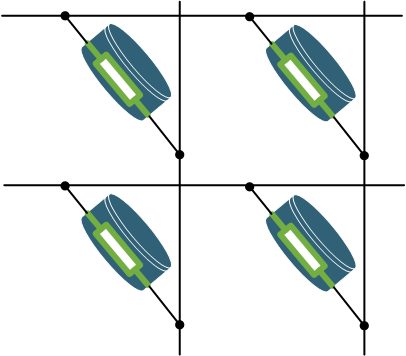
To integrate crossbars, which perform their computation in the analog domain, into a digital environment it is necessary to convert digital inputs into an analog signal (voltage or current) and convert analog outputs back to digital signals. The necessary converters then often are the energy and latency bottleneck of the system, especially if high precision is required.
Literature
| Title | Author | Year |
| Toward memristive in-memory computing: principles and applications | Bao, H., Zhou, H., Li, J. et al. | 2022 |
| Memory devices and applications for in-memory computing | Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. et al. | 2020 |
| A Review of In-Memory Computing Architectures for Machine Learning Applications | Bavikadi, S., Sutradhar, P., Khasawneh, K. et al. | 2020 |
