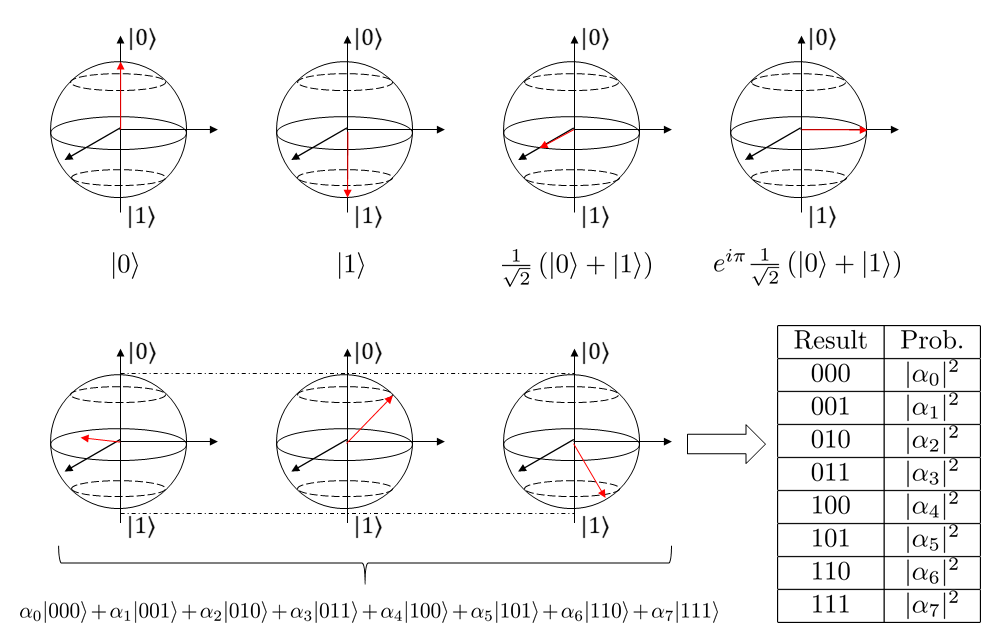
Quantum computing is a computing approach, which uses the quantum nature of a physical system to perform calculations. The basic element of a quantum computer are quantum bits, so called qubits, which are effective two-level systems from a quantum physical perspective. That means they have two states, \(|0\rangle\) and \(|1\rangle\), which are the quantum analogs to classical bit states 0 and 1. However, due to their quantum nature, qubits cannot only be in one of these two states, but also in a superposition between both of them, see fig. 1 for an illustration. In addition, the different qubits can be entangled, so that they form a complex, inseparable state. That is, the complete state can not be constructed by regarding the qubits independent of each other. By exploiting this entanglement, one can easily describe states, which cannot be represented by classical computing by using just a few qubits. Thus, quantum computers are supposed as ideal tool for simulating quantum systems, various optimization tasks, cryptography, machine learning and more.
Currently, different approaches for the physical realization of quantum computers are investigated. Some of them use quantum particles like ions, atoms, or photons while others are based on artificial quantum systems like superconducting resonating circuits. To use these systems as a computer the qubits are physically manipulated by lasers, electromagnetic fields or similar. From a programmer’s perspective this is represented by performing gates. A program running on a universal quantum computer is thus a sequence of gates acting on the qubits, which is represented as a quantum circuit. At the end of the calculation, a measurement process takes place, returning a statistical distribution representing the probabilities of the quantum mechanical state of the system, which is used for further conventional calculations. Thus, quantum computation belongs to the category of statistical compuing. The current challenge for quantum computing is, to reduce the error of the qubit manipulation and the measurement as well as scaling up the entire system to a larger number of qubits.
Beside of this gate based or universal quantum computing, there exists so called adiabatic quantum computing or quantum annealing. In this concept, the quantum computer is prepared in a state which is simple to realize. Afterwards, the system undergoes a time evolution until it approaches the state with lowest energy, the so-called ground state which can be significantly more complex. This approach is described in more detail here.
A small dive-in: More background information
Back in 1982 Richard Feynman suggested that a computer made from quantum systems should be used to simulate quantum systems and thus started the development of quantum computers [1]. Today, the first universal commercial quantum computers are available and prove the feasibility of such computations. Besides this obvious application Feynman suggested, the development of the Shor and Grover algorithm in the 1990’s showed that quantum computers can outperform conventional computers in terms of runtime in prime factor decomposition and search, respectively. Since then, especially within the last years, a larger number of applications and software was developed, which, however, is not the scope of this article.
For the physical realization of a quantum computer, David DiVincenzo developed five criteria, which a system has to fulfil [2]:
- It has to be scalable in the number of qubits
- An initialization to arbitrary states must be possible
- The performance of quantum gates must be significantly faster than the decoherence time
- A universal gate set must be available on the qubits
- The final states must be easily readable
Based on these criteria one can identify different elements of a quantum computer. The elementary element are the qubits, i.e. quantum objects, which behave as two-level systems. The universal gate set requires the possibility to manipulate the state of those qubits. That is at least some single qubit manipulation (single qubit gates) and entangling operations, which connect at least two qubits (multi qubit gates). It was shown that all possible quantum operations can be made up from a minimum of three operations [3]. With this gate set, the initialization to arbitrary states is possible. When, based on these operations, the system is in an excited state, it has the natural tendency to go back into the ground state after some time. The decoherence time is a measure to describe this live span of excited states, so that all operations on the qubits have to be significantly faster. Finally, to obtain results from the quantum computer, a quantum measurement has to be performed on the system and transferred to digital data. As a quantum measurement is performed, the same set of quantum operations (quantum circuit) has to be run several times, in order to obtain a representative quantum statistics.
In reality, quantum computers have been realized in different physical systems such as superconducting circuits, trapped ions, trapped atoms or photons. In upcoming more detailed articles, the three different elements for each system will be discussed: realization of the qubits, realization of gates on these qubits and realization of the measurement. Due to the completely different basis, a large class of technologies can be used for the creation of qubits, e.g. laser technology, electromagnetic fields or lithography, or the realization of gates e.g. lasers, electromagnetic pulses, optical elements and more, which makes the realization of quantum computers a truly multi-disciplinary approach.
To compare the realizations of quantum computers, different aspects have to be considered. First, as gates are physical manipulations of a quantum state, there is always a probability that it does not yield the requested effect. Thus, the fidelities of single and multi-qubit gates are an important measure. Second, due to the noise of each gate, the quantum volume refers to the maximal size of a square code, which is a circuit of the same number of layers as the number of qubits, which can be run and provides the correct result up to a specified probability. Third, each system has a specific decoherence time and each gate requires some time, such that this relation determines the maximal length of the circuit which can be performed on the computer. Thus, the circuit layer operations per second CLOPS determine on the one hand, the length of a circuit which can reasonably performed within the decoherence time and on the other hand, how long a circuit will take, as the circuit has to be repeated several times.
Further Reading:
| Title | Author | Year | |
| [1] | Simulating physics with computers | R. P. Feynman | 1982 |
| [2] | The physical implementation of quantum computation | D. P. DiVincenzo | 2000 |
| [3] | Quantum Computing: Progress and Prospects | E. Grumbling, M. Horowitz | 2019 |
